Contents
- 1 Empty set
- 2 Examples of empty set
- 3 Difference between a Zero Set and an Empty Set
- 4 Properties of the Empty Set
- 4.1 (1) The empty set is the subset of every set
- 4.2 (2) Union of a Set X with the Empty Set
- 4.3 (3) Intersection of a Set X with the Empty Set
- 4.4 (4) Cardinality of the Empty Set
- 4.5 (5) Cartesian product of a Set P with the Empty Set
- 4.6 (6) The power of the empty set is the set containing only the empty set
- 4.7 (7) Every non – Empty set has at least two subsets one an Empty set and other itself
- 4.8 (8) Complement of the Empty Set
- 4.9 (9) Empty set treated as Solution Set
- 5 Representation of the Empty Set by Venn Diagram
Empty set
In previous article we have learnt about Definition of Set and Methods of representation of set, in this article we are going to learn about Definition of Empty Set.
- A set which does not contain any element is called the empty set or the null set or the void set
- The empty set is denoted by A = ϕ or L= { } or Empty set = { }
- In other word we can say the empty set is a set with no elements
Download Set Theory Class 11 NCERT – Download
Examples of empty set
(1) A= {x:x2=16, x is odd integer}, P = {x:x3=27, x is negative integer}
Here Set A is the empty set or a null set, because the equation x2=16 is not satisfied by any odd integer (odd value of x)
Here Set P is the empty set or a null set, because the equation x3=27 is not satisfied by any negative integer (Negative value of x)
(2) Let Q = {x:4<x<5, x is a integer},
Here Set Q is the empty set or a null set, because there is no any integer lies between numbers 4 and 5.
(3) Let R = {x :7< x < 8, x is a natural number},
Here Set R is the empty set or a null set, because there is NO natural number lies between numbers 7 and 8.
(4) Let Z = ϕ = {x: x is multiple of 7 and 45< x <49},
Here Set Z is the empty set or null set, because there is no any number which is multiple of 7 and lies between numbers 45 and 49.
(5) E = Empty set = { } = {x: x is an odd natural number and divisible by 8},
Here Set E is the empty set or null set, because there is no any odd natural number which is divisible by 8.
Difference between a Zero Set and an Empty Set
Many students have confusion about Zero Set and they called Zero Set as Empty Set. But this is not true.
So, what is right?
So, answer is, the empty set contains no element and a Zero Set contains a Zero as an Element
In other words we can say that an Empty Set have element less feature but a Zero Set have feature with one element that is one Zero
Examples
X = {x: x is whole number and x<1}
Y = {x: x is a natural number and 6<x<7}
Here Set X can be denoted as X = {0}, because a whole number less then 1 is Zero So, Set X is a Zero Set
Here Set Y can be denoted as Y = { }, because there is no any natural number which is lies between numbers 6 and 7 so Set Y is the Empty Set
So, we can conclude this as
{0} ≠ { }.
Properties of the Empty Set
(1) The empty set is the subset of every set
The Empty set is the Subset of every set
Let Set P = {1,2,3}
We can write all possible subset of Set P
We know the number of possible subsets of Set P is 2^3 = 8
They are, {1}, {2}, {3}, {1,2}, {1,3}, {2,3}, {1,2,3}
We have written 7 subsets of Set P and one more subset of Set P will be Empty set that is ϕ
(2) Union of a Set X with the Empty Set
Union of a Set X with the Empty Set will be the Set X itself
X U ϕ = X
We know that the empty set contains no elements at all, its union with any set X produces the same set X
(3) Intersection of a Set X with the Empty Set
Intersection of a Set X with the Empty Set will be the Empty Set
X ∩ ϕ = ϕ
Example
X = {1,2,3,4}
Φ = { }
X ∩ ϕ = this will produce a set with Elements Common in Set X and ϕ
Set X contains four element 1,2,3,4 and Set ϕ contains no element
So, X ∩ ϕ = { } = ϕ
(4) Cardinality of the Empty Set
Cardinality is defined as total number of elements in the set, we know that the Empty Set has no elements so Cardinality of the Empty Set is Zero
If A = { } = ϕ
So, cardinality of set A = | A | = 0
Example
Let’s calculate the cardinality of Set P = {x: x is prime number and 6<x<7},
Here Set P is the Empty Set because there is no any prime number lies between numbers 6 and 7.
So, P = { } = ϕ
And cardinality of Set P, | P | = 0
(5) Cartesian product of a Set P with the Empty Set
Cartesian product of a Set x with the Empty set will always be the Empty set.
P ✕ ϕ = ϕ
(6) The power of the empty set is the set containing only the empty set
P(ϕ) = 2^ϕ = {ϕ}
(7) Every non – Empty set has at least two subsets one an Empty set and other itself
A = {1}
Subsets of Set A are ϕ and {1}.
(8) Complement of the Empty Set
If X and Y are two sets, then the relative complement of X in Y, written as Y − X or Y\X, or X’ is the set of elements in Y, which do not belong to X
If X and Y are two sets, then the relative complement of Y in X, written as X − Y or X\Y, or Y’ is the set of elements in X, which do not belong to Y
Let X = {a, e, i, o, u} and Y = {a, b, c, o, u}
So,
X’ = Elements in Y which do not belong to X = {b, c}
Y’ = Elements in X which do not belong to Y = {e, i}
Similarly, if we have two sets U (Universal Set) and Φ (Empty Set)
And lets universal set as U = {1,2,3,4,5,7,8}
Φ’ = U – Φ = Elements in U which do not belongs to Φ = U
Because every element in U does not belongs to Φ
So, the complement of an empty set is the universal set.
Φ’ = U
(9) Empty set treated as Solution Set
If any mathematical problem has no solution so we can represent answer of that mathematical problem in the form of Empty Set { }
Example
Find the real roots for quadratic equation x^2 + 7 = 0
We know that this quadratic equation has no any real solution, so we can represent answer as Empty set
x = ϕ
Representation of the Empty Set by Venn Diagram
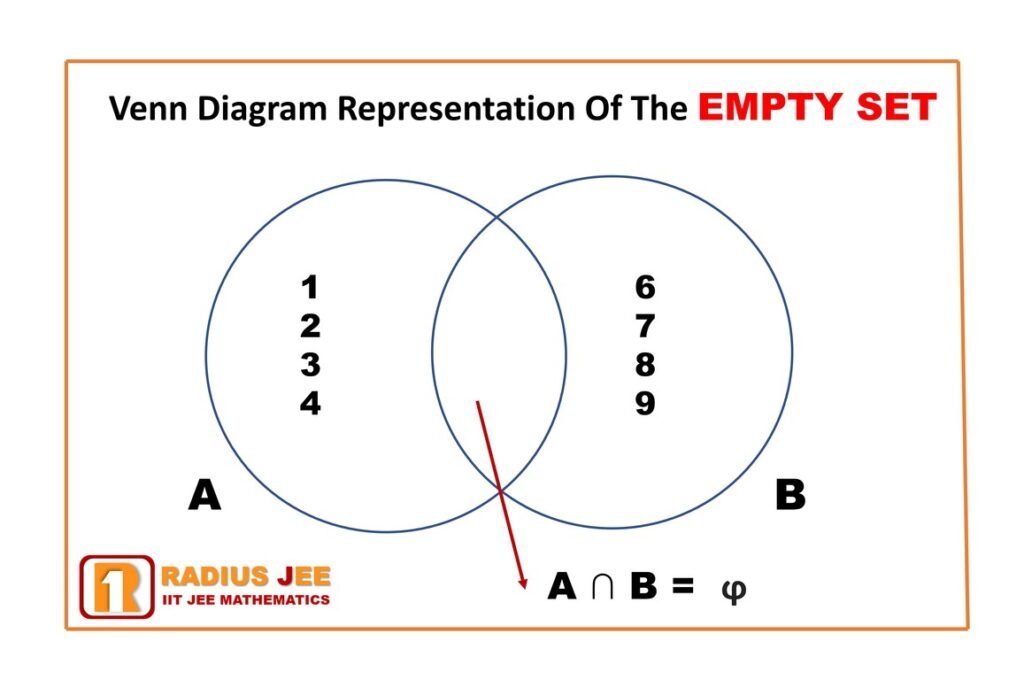
Empty Set
The Empty Set can be represented by Venn Diagram and the relation of intersection between two Sets A and B
Let A = {1, 2, 3, 4,} and B = {6, 7, 8, 9}
So, intersection of set A and set B will be the Empty set ϕ, because there is no any common element listed in set A and set B
A ∩ B = ϕ

Radis JEE Coaching in Lucknow
LINKS
0 Comments